Matte ha scritto:Come immaginavo la realtà, come spesso accade, è molto più complessa di quello che potrebbe sembrare

Se quindi voglio ad esempio calcolare la probabilità di avere esattamente una fonte di mana di un certo tipo, presente in 14 copie nel mazzo, in mano iniziale, posso usare la formula che hai riportato considerando:
a = 14
n = 60
r = 7
x = 1
Così facendo però ottengo un'improbabile probabilità del 34% e mi sa che non ho capito

No, hai fatto il calcolo perfettamente e viene proprio 34%

Considera che inserendo quei dati lì, il risultato finale è la probabilità di avere
esattamente 1 fonte di mana di quel tipo, che significa che una mano con 0 o con 2 fonti di mana è esclusa dal risultato. Significa che una partita su 3, in media, la inizierai con una e una sola di quelle fonti di mana.
---------------------------------------------------------
Consiglio per tutti: giocherellare con la distribuzione ipergeometrica in questo modo può dare risultati veramente importanti per il deckbuilding!
Sulla base della domanda di Matte, vi pongo un esempio molto significativo:
- Gioco un mazzo


piuttosto competitivo, ma non possiedo terre doppie, e mi devo arrangiare con Isole e Pianure (in totale 24)
- Il mio mazzo gioca spell ultra-intensive come
Cryptic Command,
Deprive e voglio che
Snapcaster Mage possa giocarle di nuovo (quindi mi serve molto mana

)
- Al contrario, le mie spell bianche come
Restoration Angel e
Blade Splicer non sono mana-intensive e ho notato che una sola Pianura basta a sopperire tutto il mio bisogno di mana bianco
Problema: qual è la migliore combinazione di
Isola e
Pianura, tale da giocare più partite possibile con tante isole e una sola pianura, manabase che mi permetterebbe di poter giocare qualsiasi cosa?
La soluzione sta nel considerare sia
la probabilità di pescare una sola pianura in prima mano che
il miglior rapporto Isola/Tot.Terre possibile, in modo da non finire in flood di pianure nelle pescate successive! Procediamo partendo dai dati raccolti nel post precedente:
14 Pianure + 10 Isole = 34% di una sola pianura in prima mano -> Rapporto Isola/Terre = 10/24 = 0.41. Componendo i dati raccolti (34 x 0.71) troviamo una distribuzione generale del mana non troppo soddisfacente (
13.94). Ma d'altronde non ci voleva un genio per capire che un mazzo prevalentemente blu non può girare con 14 pianure e solo 10 isole...
Però così vi ho spiegato come funziona il ragionamento: ora bisogna solo diminuire il numero di pianure pian piano (aumentando ovviamente il rapporto Isola/Terre) fino a trovare il risultato migliore!
-
13  , 11
, 11  = 36% di mono-pianura -> Rapporto = 0.458 -> Distribuzione finale 36 x 0.458 = 16.488
= 36% di mono-pianura -> Rapporto = 0.458 -> Distribuzione finale 36 x 0.458 = 16.488 -
12  , 12
, 12  = 38% di mono-pianura -> Rapporto = 0.500 -> Distribuzione finale 38 x 0.500 = 19.000
= 38% di mono-pianura -> Rapporto = 0.500 -> Distribuzione finale 38 x 0.500 = 19.000 -
11  , 13
, 13  = 40% di mono-pianura -> Rapporto = 0.541 -> Distribuzione finale 40 x 0.541 = 21.640
= 40% di mono-pianura -> Rapporto = 0.541 -> Distribuzione finale 40 x 0.541 = 21.640 -
10  , 14
, 14  = 41% di mono-pianura -> Rapporto = 0.583 -> Distribuzione finale 41 x 0.583 = 23.903
= 41% di mono-pianura -> Rapporto = 0.583 -> Distribuzione finale 41 x 0.583 = 23.903 -
9  , 15
, 15  = 42% di mono-pianura -> Rapporto = 0.625 -> Distribuzione finale 42 x 0.625 = 26.250
= 42% di mono-pianura -> Rapporto = 0.625 -> Distribuzione finale 42 x 0.625 = 26.250 -
8  , 16
, 16  = 42% di mono-pianura -> Rapporto = 0.666 -> Distribuzione finale 42 x 0.666 = 27.972
= 42% di mono-pianura -> Rapporto = 0.666 -> Distribuzione finale 42 x 0.666 = 27.972 -
7  , 17
, 17  = 41% di mono-pianura -> Rapporto = 0.708 -> Distribuzione finale 41 x 0.708 = 29.028
= 41% di mono-pianura -> Rapporto = 0.708 -> Distribuzione finale 41 x 0.708 = 29.028 -
6  , 18
, 18  = 40% di mono-pianura -> Rapporto = 0.750 -> Distribuzione finale 40 x 0.750 = 30.000
= 40% di mono-pianura -> Rapporto = 0.750 -> Distribuzione finale 40 x 0.750 = 30.000 -
5  , 19
, 19  = 37% di mono-pianura -> Rapporto = 0.791 -> Distribuzione finale 37 x 0.791 = 29.267
= 37% di mono-pianura -> Rapporto = 0.791 -> Distribuzione finale 37 x 0.791 = 29.267Abbiamo quindi trovato il picco della parabola! Notando che già con 5 pianure la nostra stabilità di mana inizia a peggiorare, si può immaginare che proseguendo così arriveremo a risultati più brutti... Quindi tiriamo le somme!
Un mazzo impostato come da ipotesi avrà la manabase migliore possibile se giochiamo
6 Pianure e
18 Isole, con una possibilità di pescare una sola pianura in prima mano di 40% e con 3 Isole nel mazzo per ogni pianura, in media.
D'altronde anche gli approcci "a occhio" funzionano alla grande: come potete avere il mana per lanciare un
Cryptic Command oppure un
Restoration Angel? solo in un modo,




, ovvero proprio 3 isole per 1 pianura, quello che abbiamo trovato noi

EDIT: Mentre rispondevo, Matte ha editato il suo vecchio messaggio, quindi non preoccupatevi se la mia citazione vi sembra "strana"







 , vorrei aggiungermi e fare una domanda simile.
, vorrei aggiungermi e fare una domanda simile. 

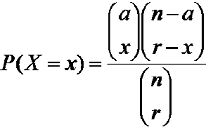



 piuttosto competitivo, ma non possiedo terre doppie, e mi devo arrangiare con Isole e Pianure (in totale 24)
piuttosto competitivo, ma non possiedo terre doppie, e mi devo arrangiare con Isole e Pianure (in totale 24)